Частота (англ.
Frequency) — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения
F - Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (
Гц, Hz ). Величина, обратная частоте, называется периодом.

Содержание
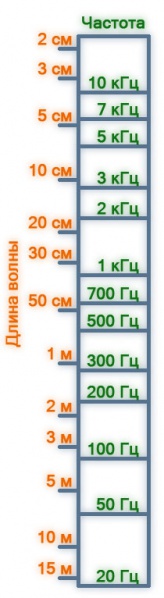
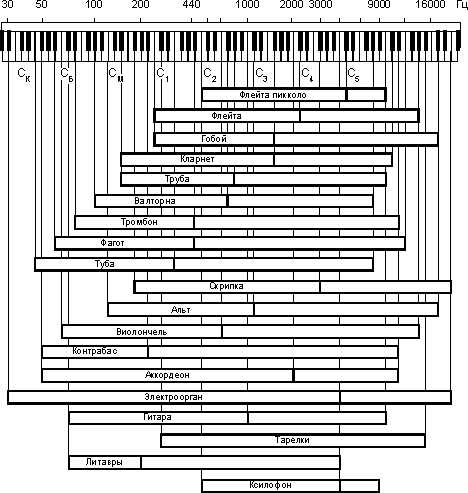
Наше ухо способно реагировать на сравнительно небольшую полосу (участок) частот звуковых колебаний - примерно от 20 Гц до 20 кГц. Эта полоса вмещает всю обширнейшую гамму звуков, создаваемых голосом человека и симфоническим оркестром: от очень низких тонов, похожих на звук грома при грозе , до еле уловимого высокого писка комара. Колебания частотой до 25 Гц, называемые инфразвук, и свыше 20 кГц, называемые ультразвук, мы не слышим. А если б наше ухо оказалось способным реагировать и на ультразвуковые колебания, мы, возможно, могли бы слышать колебания пестиков цветов, крылышек бабочек.А при грозе многие инфразвуковые составляющие грома мы чувствуем , а не слышим .При этом могут возникать панические настроения . Автомобильная звуковая система должна воспроизвести весь слышимый диапазон частот с равномерной АЧХ при помощи CD-ресивера , усилителя и АС .В описании характеристик аппаратуры присутствуют данные о диапазоне воспроизводимых частот .Чаще это выглядит так : 50 гц - 20 кгц .При этои должна быть указана неравномерность АЧХ . То есть аппарат воспроизводит звук с такой частотой , те же 50 гц , но намного тише , чем 1 кгц ,например . Если этого нет , то таким данным нельзя доверять .
[hide][top]Мгновенная частота и частоты спектральных составляющих
Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка.
В теории электромагнетизма, теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается

). Циклическая частота связана с частотой колебаний соотношением

. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в (
рад/с,
rad/s) .
В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.
[hide][top]Частота дискретных событий
Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (с−1, s−1), однако на практике для выражения частоты импульсов обычно используют герц.
Частота вращения — физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с−1, s−1), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.
[hide][top]Метрологические аспекты
- Для измерения частоты применяются частотомеры разных видов, в том числе: для измерения частоты импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра.
- Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот, генераторы сигналов и др.
- Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу.
 Наше ухо способно реагировать на сравнительно небольшую полосу (участок) частот звуковых колебаний - примерно от 20 Гц до 20 кГц. Эта полоса вмещает всю обширнейшую гамму звуков, создаваемых голосом человека и симфоническим оркестром: от очень низких тонов, похожих на звук грома при грозе , до еле уловимого высокого писка комара. Колебания частотой до 25 Гц, называемые инфразвук, и свыше 20 кГц, называемые ультразвук, мы не слышим. А если б наше ухо оказалось способным реагировать и на ультразвуковые колебания, мы, возможно, могли бы слышать колебания пестиков цветов, крылышек бабочек.А при грозе многие инфразвуковые составляющие грома мы чувствуем , а не слышим .При этом могут возникать панические настроения . Автомобильная звуковая система должна воспроизвести весь слышимый диапазон частот с равномерной АЧХ при помощи CD-ресивера , усилителя и АС .В описании характеристик аппаратуры присутствуют данные о диапазоне воспроизводимых частот .Чаще это выглядит так : 50 гц - 20 кгц .При этои должна быть указана неравномерность АЧХ . То есть аппарат воспроизводит звук с такой частотой , те же 50 гц , но намного тише , чем 1 кгц ,например . Если этого нет , то таким данным нельзя доверять .
Наше ухо способно реагировать на сравнительно небольшую полосу (участок) частот звуковых колебаний - примерно от 20 Гц до 20 кГц. Эта полоса вмещает всю обширнейшую гамму звуков, создаваемых голосом человека и симфоническим оркестром: от очень низких тонов, похожих на звук грома при грозе , до еле уловимого высокого писка комара. Колебания частотой до 25 Гц, называемые инфразвук, и свыше 20 кГц, называемые ультразвук, мы не слышим. А если б наше ухо оказалось способным реагировать и на ультразвуковые колебания, мы, возможно, могли бы слышать колебания пестиков цветов, крылышек бабочек.А при грозе многие инфразвуковые составляющие грома мы чувствуем , а не слышим .При этом могут возникать панические настроения . Автомобильная звуковая система должна воспроизвести весь слышимый диапазон частот с равномерной АЧХ при помощи CD-ресивера , усилителя и АС .В описании характеристик аппаратуры присутствуют данные о диапазоне воспроизводимых частот .Чаще это выглядит так : 50 гц - 20 кгц .При этои должна быть указана неравномерность АЧХ . То есть аппарат воспроизводит звук с такой частотой , те же 50 гц , но намного тише , чем 1 кгц ,например . Если этого нет , то таким данным нельзя доверять . ). Циклическая частота связана с частотой колебаний соотношением
). Циклическая частота связана с частотой колебаний соотношением  . В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в (рад/с, rad/s) .
. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в (рад/с, rad/s) . (0) Отзывы про: Частота
(0) Отзывы про: Частота 
Социальные закладки